| A 1.0 |
Die Parabel p hat die Gleichung y = -0,25x2 + 3x - 1 mit G = IRxIR.
Die Gerade g hat die Gleichung y = -0,25x + 4,5 mit G = IRxIR.
|
|
| A 1.1 |
Zeichnen
p mit y = -0,25x 2 + 3x - 1
| x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| y |
-1 |
1,75 |
4 |
5,75 |
7 |
7,75 |
8 |
7,75 |
7 |
5,75 |
4 |
1,75 |
-1 |

Sie für die Parabel p eine Wertetabelle für x ∈ [0;12] in Schritten von Δx = 1 und zeichnen Sie sodann die
Parabel p und die Geraden g in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm; -1 ≤ x ≤ 13 -2 ≤ y ≤ 9
|
3 P |
| A 1.2 |
Die Punkte Mn(x | -0,25x + 4,5) auf der Geraden g sind die Mittelpunkte der Basis [AnBn] von
gleichschenkligen Dreiecken AnBnCn mit xA < xB.
Es gilt: [AnBn] || x-Achse und AnBn = 4LE 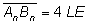 . .
Die Punkte Cn(x | -0,25x2 + 3x - 1)
liegen auf der Parabel p und haben dieselbe Abszisse x
wie die Punkte Mn.
Zeichnen
Für die Zeichnung der gleichschenkligen Dreiecke benötigst du folgende Eigenschaften:
[A nB n] ⊥ [C nM n] und AnBn = 2 · AnMn .

Sie das Dreieck A1B1C1 für x = 4 und A2B2C2
für x = 10 in das Koordinatensystem zu 1.1 ein.
Zusätzlicher Service:
Dynamische Zeichnung
|
3 P |
| A 1.3 |
Ermitteln

|
Es existiert kein Dreieck
AnBnCn mehr,
wenn die Punkte Mn und Cn
zusammenfallen.
(vgl. Zeichnung). Nimmt anschließend x
noch kleinere Werte an,
so entstehen zwar wieder Dreiecke, die jedoch dann
AnCnBn lauten.
Anhand der dynamischen Zeichnung aus 1.2 kannst du dir dies noch einmal verdeutlichen.
Also liefern die x-Werte der Schnittpunkte der Parabel p
mit der Geraden g die Grenzen des gesuchten Intervalls.
Damit lautet der Ansatz:
|
- 0,25x2 + 3x - 1 = - 0,25x + 4,5 G = IR.
⇔ - 0,25x2 + 3,25x - 5,5 = 0
Für die Diskriminante D = b2 - 4ac
ergibt sich somit
D = 3,252 - 4 · (-0,25) · (-5,5) = 5,0625
|
Durch Anwenden der Lösungsformel x1/2 =
|
-b ± D
| | 2 · a |
| erhält man x1/2 =
|
-3,25 ± 5,0625
| | 2 · (-0,25) |
⇔ x = 2 ∨ x = 11 ⇒ IL = {2;11}
Das gesuchte Intervall lautet somit: 2 < x < 11
|
Sie rechnerisch das Intervall für die Abszisse x der Punkte Mn so, dass Dreiecke AnBnCn
existieren.
|
3 P |
| A 1.4 |
Berechnen

|
Die Punkte Cn und Mn besitzen laut Angabe stets die gleiche Abszisse (x-Wert).
Daher kann man die Länge der Strecke [MnCn] durch Subtraktion der y-Koordinaten der Punkte Cn und
Mn erhalten.
|
yC - yM
= - 0,25x2 + 3x - 1
- (- 0,25x + 4,5)
yC - yM
= - 0,25x2 + 3x - 1 + 0,25x - 4,5
yC - yM
= - 0,25x2 + 3,25x - 5,5
Somit gilt:
MnCn (x) = (-0,25x2 + 3,25x - 5,5) LE
|
Sie die Länge der Strecke [MnCn] in Abhängigkeit von der Abszisse x der Punkte Mn.
[Teilergebnis: MnCn (x) = (-0,25x2 + 3,25x - 5,5) LE ]
|
1 P |
| A 1.5 |
Unter den Dreiecken AnBnCn
hat das Dreieck A0B0C0
den größtmöglichen Flächeninhalt.
Bestimmen

|
Den Flächeninhalt A(x) der
Dreiecke AnBnCn bestimmst du mit Hilfe
der Formel:
A(x) = 1/2 ·
AnBn ·
MnCn
Dabei ist
MnCn (x) = (-0,25x2 + 3,25x - 5,5) LE
und laut Angabentext
AnBn = 4 LE
|
Damit ergibt sich:
A(x) = 1/2 · 4
· (
- 0,25x2 + 3,25x - 5,5) FE
A(x) = 2 · (- 0,25x2 + 3,25x - 5,5) FE
A(x) = (- 0,5x2 + 6,5x - 11) FE
Zur Bestimmung von Amax betrachte ich:
T(x) = - 0,5x2 + 6,5x - 11
T(x) = - 0,5[x2 - 13x] - 11
T(x) = - 0,5[(x2 - 13x + 6,52) - 6,52] - 11
T(x) = - 0,5[(x - 6,5)2 - 42,25] - 11
T(x) = - 0,5(x - 6,5)2 + 21,13 - 11
Damit ist Amax = 10,13FE
|
Sie den größtmöglichen Flächeninhalt Amax
auf zwei Stellen nach dem Komma gerundet.
|
3 P |
| A 1.6 |
Für die Punkte C3 und C4 sind die Dreiecke
A3B3C3 und
A4B4C4 gleichseitig.
Berechnen

|
In gleichseitigen Dreiecken gilt für die
Höhe in Bezug auf die Seitenlängen der Zusammenhang:
h = a/2 · 3
Für unsere Aufgabe bedeutet dies:
AnBn = 4 LE
⇒
MnCn = 2 · 3 LE = 3,46 LE
Zugleich gilt aber:
[MnCn] in Abhängigkeit von der Abszisse x der Punkte Mn
|
|
MnCn = (-0,25x2 + 3,25x - 5,5) LE
Daher kann ich zur Berechnung von x die beiden Zahlenterme gleichsetzten:
|
- 0,25x2 + 3,25x - 5,5 = 3,46
⇔ - 0,25x2 + 3,25x - 8,96 = 0
Für die Diskriminante D = b2 - 4ac
ergibt sich somit
D = 3,252 - 4 · (-0,25) · (-8,96) = 1,6025
|
Durch Anwenden der Lösungsformel x1/2 =
|
-b ± D
|
|
2 · a
|
|
erhält man x1/2 =
|
-3,25 ± 1,6025
|
|
2 · (-0,25)
|
⇔ x = 3,97 ∨ x = 9,03 ⇒ IL = {3,97 ; 9,03}
Da die Punkte C3 und C4 auf der Parabel
p mit y = -0,25x2 +3x - 1 liegen, gilt:
C3(3,97 | -0,25 · 3,972 +3 · 3,97 - 1); C3(3,97 | 6,97)
C4(9,03 | -0,25 · 9,032 +3 · 9,03 - 1); C3(9,03 | 5,70)
|
Sie die x-Koordinaten der Punkte C3 und C4.
(Auf zwei Stellen nach dem Komma runden.)
[Teilergebnis:
M3C3 = M4C4 = 2 · 3 LE ]
|
4 P |