| A 2.0 |
Die Firma Maier erhält von der Messeleitung ein dreieckiges Grundstück ABC auf dem Messegelände zugewiesen, auf dem sie ihren Informationspavillon
errichten kann. Der Pavillon hat eine kreisförmige Grundfläche und wird so auf die Dreiecksgrundfläche gestellt, dass seine Grundfläche die drei Seiten des
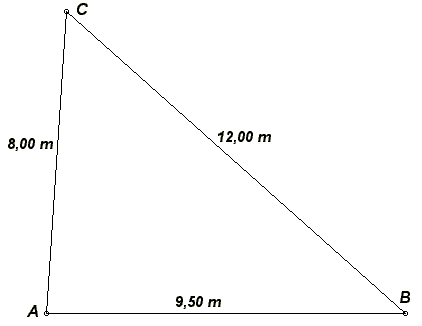
Grundstücks ABC berührt. Das Dreieck ABC hat die Seitenlängen
AB = 9,50m ,
AC = 8,00m und BC = 12,00m.
Hinweis für Berechnungen:
Runden Sie jeweils auf zwei Stellen nach dem Komma:
Winkelmaße in °, Längen in m und Flächeninhalte in m2.
|
|
| A 2.1 |
Berechnen
Zur Berechnung der Winkelmaße verwendest du den Kosinussatz.
|
cosα =
|
AB2 + AC2 - BC2
|
|
2 · AB · AC
|
cosα = 9,502 + 8,002 - 12,002/2 · 9,50 · 8,00 ⇒ α = 86,13°
|
cosβ =
|
AB2 + BC2 - AC2
|
|
2 · AB · BC
|
cosβ = 9,502 + 12,002 - 8,002/2 · 9,50 · 12,00 ⇒ β = 41,69°
Sie das Maß α des Winkels BAC und das Maß β des Winkels CBA des Dreiecks ABC.
Zeichnen Sie das dreieckige Grundstück ABC im Maßstab 1:100.
[Teilergebnis: α= 86,13° ; β = 41,69°]
|
3 P |
| A 2.2 |
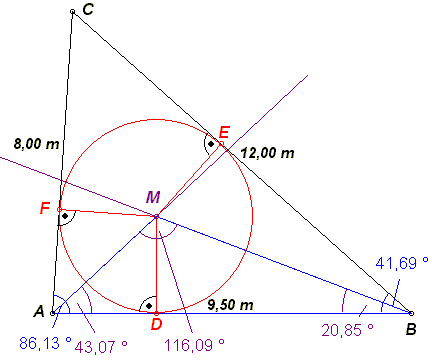
Die Winkelhalbierenden der Winkel BAC und CBA schneiden sich im Punkt M. Der Fußpunkt des Lotes von M auf die Seite [AB] ist der Punkt D,
von M auf [BC] der Punkt E und von M auf [AC] der Punkt F.
Zeichnen Sie die beiden Winkelhalbierenden und tragen Sie die Punkte M, D, E und F sowie die kreisförmige
Pavillongrundfläche in die Zeichnung zu 2.1 ein.
Ermitteln
|
Den Radius [MD] kannst du z. B. im rechtwinkligen Dreieck ADM berechnen.
Da du wegen der Winkelhalbierenden des Winkels BAD bereits das Maß
des Winkels ∡DAM = 43,07°
kennst, fehlt noch eine Seitenlänge, um den Radius berechnen zu können.
|
Die Länge der Strecke [AM] kann dazu im Dreieck ABM
berechnet werden. Dabei gilt:
∡AMB = 180° - 43,07° - 20,85°
∡AMB = 116,09°
Mit dem Sinussatz im ΔABM folgt:
AM/sin20,85° = AB/sin 116,09°
AM = 9,50m/sin 116,09° · sin 20,85°
AM = 3,76m
|
Nun kannst du im rechtwinkligen Dreieck ADM den Radius [MD] mit dem Sinus berechnen. Es gilt:
sin43,07° = MD/AM ⇒ MD = 3,76m · sin43,07° ⇒
MD = 2,57m
Sie sodann rechnerisch den Radius [MD] der Pavillongrundfläche.
[Teilergebnis: MD = 2,57m ]
|
4 P |
| A 2.3 |
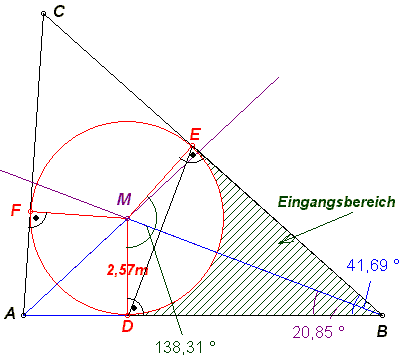
Der Eingangsbereich zum Pavillon ist die Fläche, die vom Kreisbogen 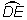 und von
den Strecken [BE] und [BD] begrenzt wird. und von
den Strecken [BE] und [BD] begrenzt wird.
Berechnen
|
Um den Flächeninhalt des Eingangsbereichs zu berechnen,
subtrahierst du vom Flächeninhalt des rechtwinkligen Drachenvierecks
DBEM
den Flächeninhalt des Sektors
DEM.
Den Winkel des Sektors kannst du im Viereck
DBEM
berechnen:
|
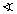 DME = 360° - 90° - 90° - 41,69° DME = 360° - 90° - 90° - 41,69°
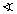 DME = 138,31° DME = 138,31°
Für den Sektor ergibt sich damit:
|
ASektor =
|
MD2 · π · 138,31°
|
ASektor = 7,97m2
|
|
360°
|
Für den Flächeninhalt des Drachenvierecks gilt:
ADBEM = 1/2
· BM · ED
Die Länge der Strecke [BM] kannst du im rechtwinkligen Dreieck
DBM
mit dem Sinus berechnen.
sin20,85° = MD/BM
⇔
BM = MD/sin20,85°
⇔
BM = 2,57m/sin20,85°
BM = 7,22m
Die Länge der Strecke [ED] kannst du im Dreieck
DEM
mit dem Kosinussatz berechnen.
ED2 =
MD2 +
ME2 -
2 · MD · ME · cos138,31° ; MD = ME = 2,57m
ED =
2,572 + 2,572 - 2 · 2,57 · 2,57 · cos138,31° m
ED = 4,80m
ADBEM = 0,5 · 7,22m · 4,80m = 17,33m2
AEingangsbereich = 17,33m2 - 7,97m2 = 9,36m2
|
Sie den Flächeninhalt dieses Eingangsbereichs.
[Teilergebnis: BD = 6,75m ]
|
4 P |
| A 2.4 |
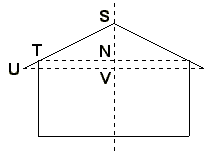
Die nebenstehende Skizze zeigt den Axialschnitt des Pavillons aus 2.0.
Der Pavillon hat die Form eines Zylinders, auf dem ein kegelförmiges Dach aufgesetzt ist. Dadurch vergrößert sich die Höhe des Pavillons um die
Länge der Strecke SN = 1,75m.
|
|
Wie viele Quadratmeter

|
Die Dachfläche des Pavillons ist die Mantelfläche des aufgesetzen Kegels, der in nebenstehendem Axialschnitt zu sehen ist.
|
Die Mantelfläche eines Kegels berechnet sich mit
der Formel:
MKegel = r · s · π.
Bei dieser Aufgabe bedeutet dies:
MKegel = UV · US · π.
Dabei ist: US = TS + TU
TS2 = TN2 + SN2
⇒
TS =
2,572 + 1,752 m
⇔ TS = 3,11m
Somit ist:
US = 3,11m + 0,10m = 3,21m
Um die Länge der Strecke [UV] (Radius!) berechnen zu können,
benötigst du den Vierstreckensatz mit Zentrum S:
UV/TN =
US/TS
⇔
UV =
3,21m · 2,57m/3,11m
⇔ UV = 2,65m
MKegel = 2,65m · 3,21m · π = 26,72m2
Es werden damit 26,72m2 Zeltplane benötigt.
|
Zeltplane werden für die Dachfläche des Pavillons benötigt, wenn das Dach des Pavillons ringsherum einen Überstand TU = 10cm haben soll (siehe Axialschnitt)?
[Teilergebnis: UV = 2,65m ]
|
4 P |