| A 2.0 |
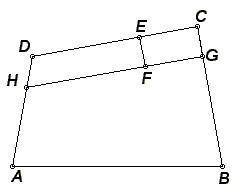
Gegeben ist das Viereck ABCD mit
AD = 6,7cm;
DC = 10,0cm;
∡BAD = 80° ;
∡ADC = 110°
und ∡DCB = 90°
Hinweis für Berechnungen:
Runden Sie jeweils auf eine Stelle nach dem Komma:
Winkelmaße in °, Längen in cm bzw. m,
Flächeninhalte in cm2 bzw. m2.
|
|
|
|
| A 2.1 |
Zeichnen

Die Länge der Strecke [AC] kannst du im ΔACD mit Hilfe des Kosinussatzes berechnen:
AC = 6,72 + 10,02 - 2 · 6,7 · 10,0 · cos110° cm AC = 13,8cm
Das Winkelmaß φ kannst du im gleichen Dreieck mit dem Sinussatz ermitteln:
sinφ/10cm = sin 110°/13,8cm
φ = 42,9° (oder φ =137,1°)
Sie das Viereck ABCD und berechnen Sie die Länge der Diagonalen [AC], sowie das Maß φ des Winkels CAD.
[Teilergebnisse: AC = 13,8cm ; φ = 42,9°]
|
3 P |
| A 2.2 |
Zeichnen Sie das Rechteck CEFG mit E ∈ [DC], F ∈ [AC], G ∈ [BC]
mit
EC = 3,5cm in die Zeichnung zu 2.1 ein und
berechnen

Die Länge der Strecke [EF] kannst Du im rechtwinkligen Dreieck EFC berechnen:
tan ∡EFC = EF/3,5cm
Dabei ist
∡ECF= ∡DCA
∡ECF = 180° - 110° - 42,9°
∡ECF = 27,1°
EF = 3,5cm · tan27,1° ⇒ EF = 1,8cm
Sie die Länge der Strecke [EF].
[Teilergebnis: EF = 1,8cm]
|
2 P |
| A 2.3 |
Die Verlängerung der Strecke [FG] über F hinaus schneidet die Seite [AD] im Punkt H.
Berechnen

Das Viereck HFED ist ein Trapez. Dabei sind [HF] und [ED] die parallelen Grundseiten und das in 2.2 berechnete
EF = 1,8cm ist die Höhe.
A Trapez = 1/2 ·
( HF + DE) ·
EF. Es ist:
HF = HN +
NF, wobei
NF = DE = 6,5cm
Im Dreieck HND gilt:
tan20° = HN/1,8cm ⇒ HN = 0,7cm
A Trapez = 1/2 · (7,2cm + 6,5cm) · 1,8cm
A Trapez = 12,3cm 2
Sie den Flächeninhalt AHFED des Vierecks HFED.
|
4 P |
| A 2.4 |
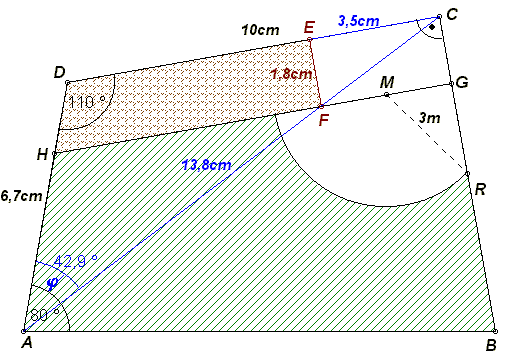
Das Viereck ABCD stellt den Plan eines Grundstücks im Maßstab 1:100 dar.
Dabei ist das Rechteck CEFG der Grundriss eines Schafstalles,
das Viereck HFED der eines Gemüsegartens und das Viereck ABGH
der einer Viehweide.
Der Punkt M ist der Mittelpunkt der Strecke [FG]. Die Strecke [HF]
markiert den Verlauf eines Zaunes zwischen Viehweide und Gemüsegarten.
An der Stelle M wird ein Schaf so mit einem Strick
angebunden, dass es alles Fressbare bis zu einer
Entfernung von 3,0 m erreichen kann.
Zeichnen Sie in die Zeichnung zu 2.1 den Bereich der
Weide ein, den das Schaf abgrasen kann und
berechnen
Für den gesuchten Flächeninhalt gilt:
AWeide = AΔGMR + ASektor.
AΔGMR =
0,5 · 3,0m · 1,8m · sin∡RMG
Zur Berechnung von ∡RMG betrachte das rechtwinkligen Dreieck RGM. Hier gilt:
cos∡RMG = MG/MR
cos∡RMG = 1,8m/3m
⇒ ∡RMG = 53,1°
AΔGMR = 0,5 · 3,0m · 1,8m · sin53,1° = 2,2m2
Für die Berechnung von A Sektor benötigst du neben dem
Radius r = 3m noch das Maß von ∡FMR.
∡FMR = 180° - 53,1° = 126,9°
A Sektor = 3,02 · π · 126,9°/360° m 2
ASektor = 10,0m2
⇒ AWeide = 12,2m2
Sie sodann seinen Flächeninhalt AWeide in Quadratmetern.
|
4 P |
| A 2.5 |
Ermitteln

Für den gesuchten Flächeninhalt ist zu beachten, dass sich der Strick,
mit dem das Schaf angebunden ist, an der Ecke F anlegt. Damit ergibt
sich für den kleinen Sektor ein neuer Radius,
nämlich r = 3m - 1,8m = 1,2m. Der Sektorwinkel misst 90°.
Somit gilt:
A Sektor = 122 · π · 90°/360° m 2
A Sektor = 1,1m 2
Sie rechnerisch den Flächeninhalt des Gemüsegartenteils, den das Schaf abweiden kann, wenn der Zaun entfernt wird.
|
3 P |