| A 2.0 |
|
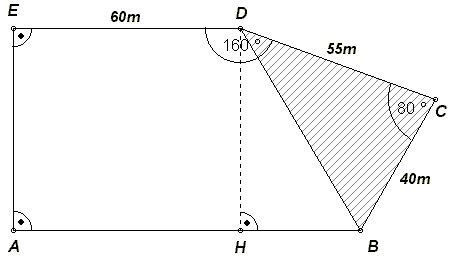
Nebenstehende Skizze zeigt den Plan eines Grundstücks auf
dem ein Freizeitgelände für Kinder angelegt werden soll.
Das Grundstück ABCDE hat die Form eines Fünfecks. Auf der
Seite [AB] befindet sich im Punkt H ein Hydrant.
|

|
Es gelten folgende Maße:
BC = 40m;
CD = 55m;
DE = 60m;
AH = 60m;
∡DCB = 80° ;
∡EDC = 160° ;
∡AED = 90° ;
∡BAE = 90° ;
∡BHD = 90°
Hinweis für Berechnungen:
Runden Sie jeweils auf eine Stelle nach dem Komma:
Winkelmaße in °, Längen in m, Flächeninhalte in m2 und Volumina in m3.
|
|
| A 2.1 |
Zeichnen

Ein geeigneter Maßstab wäre z.B. 1:1000
Damit entsprechen 40m in der Zeichnung 4cm usw.
Sie das Fünfeck ABCDE und den Punkt H in einem geeigneten Maßstab. Geben Sie den gewählten Maßstab an.
|
2 P |
| A 2.2 |
Auf der dreieckigen Teilfläche BCD soll ein Geräteparcours entstehen. Dazu wird die Teilfläche 30 cm tief ausgegraben und mit Sand gefüllt.
Wie viele
Tonnen Sand
Bei dieser Aufgabe musst du eigentlich zuerst das Volumen V Sand
eines Prismas bestimmen mit der Grundfläche A ΔBCD und der Höhe h = 30cm.
A ΔBCD = 0,5 · 40,0m · 55,0m · sin80° ;
A ΔBCD = 1083,3m2
V Sand = 1083,3m 2 · 0,3m = 325,0m 3
Da nach Angabe ein m 3 Sand eine Masse m Sand = 1,5t besitzt, ergibt sich:
m Sand = 325,0 · 1,5t = 487,5t
müssen angeliefert werden, wenn ein Kubikmeter Sand die Masse von 1,5 t hat?
|
2 P |
| A 2.3 |
Angrenzend an den Geräteparcours wird eine Rasenfläche in Form eines Kreissektors mit dem Mittelpunkt B und dem Radius BD angelegt.
Der Kreis um B mit dem Radius BD schneidet die
Seite [AB] im Punkt F.
Tragen Sie den Kreissektor BDF in die Zeichnung zu 2.1 ein und
berechnen

Um den Flächeninhalt des Kreissektors zu bestimmen, benötigst du den Radius BD und
das Maß des Winkels ∡DBF.
BD kannst du mit Hilfe des Kosinussatzes im ΔBCD berechnen.
BD = 40,02 + 55,02 - 2 · 40,0 · 55,0 · cos80° m BD = 62,1m
Das Maß des Winkels ∡DBF kannst du
nicht direkt bestimmen. Also versuchst du, zuerst im
ΔBCD den Winkel BDC zu bestimmen,
dann den Winkel HDB und schließlich
Winkel DBF.
Im ΔBCD gilt:
sin ∡DBC/40m = sin 80°/62,1m
Damit ist:
∡BDC = 39,4° (oder ∡DBF = 140,6°)
∡HDB = 160° - 90° - 39,4° = 30,6°
∡DBA = 180° - 90° - 30,6° = 59,4°
A Sektor BDF = 62,12 · π · 59,4°/360° m 2
A Sektor BDF = 1999,0m2
Sie den Flächeninhalt der Rasenfläche.
[Teilergebnisse: BD = 62,1m ; ∡DBF = 59,4°]
|
4 P |
| A 2.4 |
Die restliche Grundstücksfläche wird als Wasser-Matsch-Zone ausgewiesen.
Ermitteln

Den Flächeninhalt AWasserMatsch berechne ich, in dem ich vom Flächeninhalt des Trapezes ABDE den Flächeninhalt des Sektors BDF subtrahiere.
Für den Flächeninhalt des Trapezes brauche ich die Längen der beiden Grundlinien [ED], [AB] und die Höhe [DH]. Im ΔHBD gilt:
sin 59,4° = DH/62,10m
⇒ DH = 53,5m
Im ΔHBD gilt:
cos 59,4° = HB/62,10m
⇒ HB = 31,6m
ATrapez ABDE = 0,5 · (60m + 91,6m) · 53,5m = 4055,3m2
AWasserMatsch = ATrapez ABDE - A Sektor BDF
AWasserMatsch = 4055,3m 2 - 1999,0m 2 =
2056,3m2
p = 2056,3/5138,6 · 100 ⇒ p = 40,0
Der Anteil der Wasser- und Matschzone beträgt 40,0% der Grundstücksfläche.
Sie rechnerisch den prozentualen Anteil dieser Wasser-Matsch-Zone an der gesamten Grundstücksfläche.
[Teilergebnis: DH = 53,5m].
|
4 P |
| A 2.5 |
In einem Punkt M innerhalb der Wasser-Matsch-Zone wird eine Wasserfontäne angebracht, die bei maximalem Wasserdruck eine kreisförmige Fläche mit dem Durchmesser 30,0 m besprüht.
Dieser Kreis um M berührt die Seite [AE] im Punkt G und die Seite [ED] im Punkt K.
Zeichnen Sie die Punkte M, G und K in die Zeichnung zu 2.1 ein und
berechnen

Das Dreieck NHM ist rechtwinklig.
NM = NK - KM
NM = 53,5m - 15,0m = 38,5m
NH = AH - AN
NH = 60,0m - 15,0m = 45,0m
Aus dem Satz des Pythagoras im Dreieck NHM folgt:
HM = (38,52 + 45,02 m HM = 59,2m
Sie sodann die Länge der Wasserzuleitung [HM].
|
3 P |