| A 1.0 |
Die Gerade g1 hat die Gleichung y = 1/5 x - 4
und die Gerade g2 hat die Gleichung y = -x + 8.
|
|
| A 1.1 |
Zeichnen
Sie die Geraden g1 und g2 in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm; -1 < x < 11 ; -5 < y < 9
|
1 P |
| A 1.2 |
Punkte An(x | 0,2x - 4) und Punkte Cn auf der Geraden g2 haben jeweils die gleiche Abszisse x und sind zusammen
mit den Punkten Bn und Dn die Eckpunkte von Rauten AnBnCnDn.
Für die Diagonalen [BnDn] gilt: BnCn = x LE mit x∈]0;10[, x∈IR.
Die Maßzahl x der Diagonalenlängen ist somit gleich der Abszisse x der Punkte An und Cn.
Zeichnen
Benötigte Eigenschaft für das Zeichnen der Rauten:
Die Diagonalen einer Raute stehen aufeinander sekrecht und halbieren sich gegenseitig.
Laut Angabentext ist BnCn = x LE
also B1C1 = 2 LE und
B2C2 = 6 LE
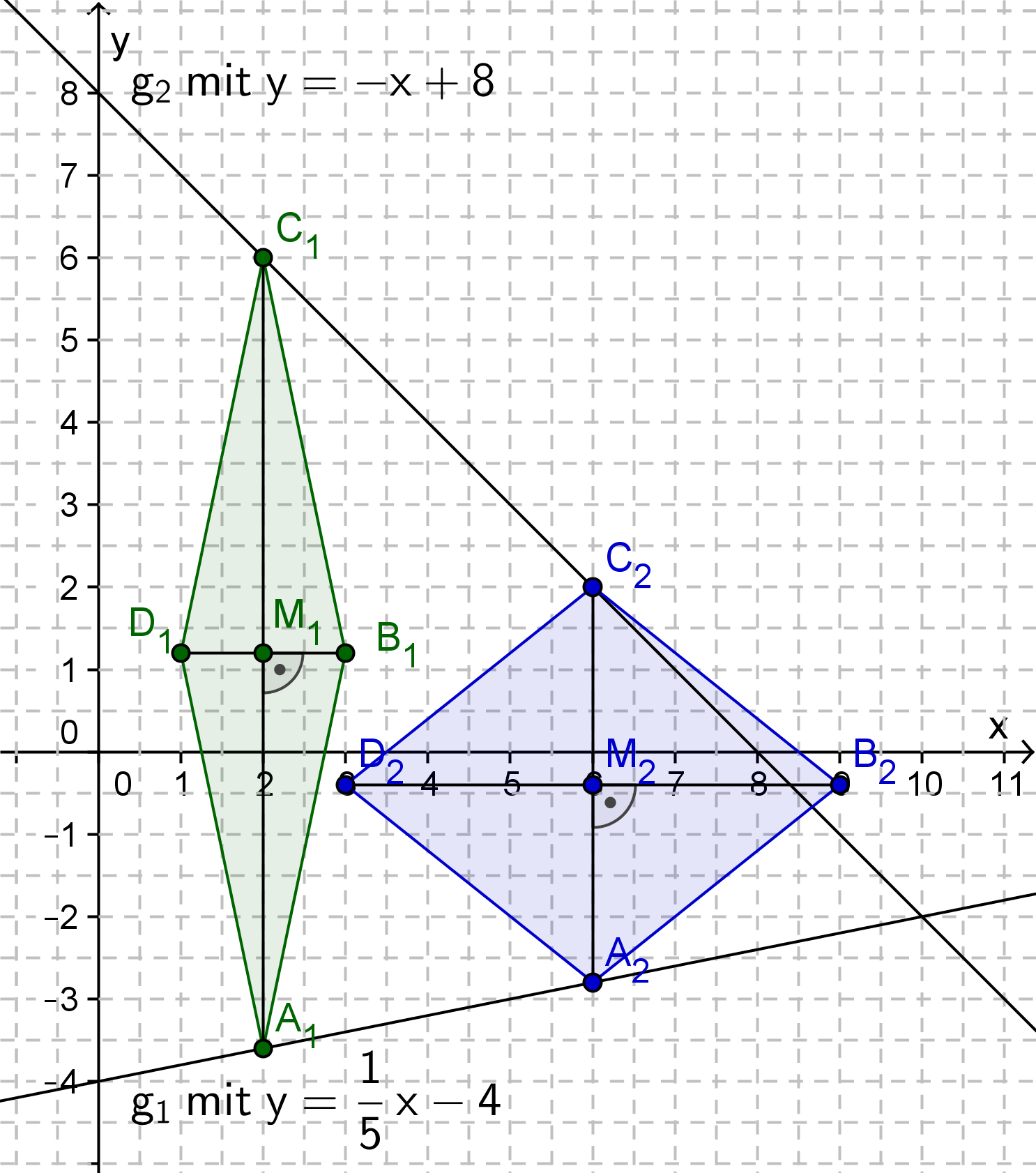
Sie die Raute A1B1C1D1 für x = 2 und die Raute A2B2C2D2
für x = 6 in das Koordinatensystem zu 1.1 ein.
|
2 P |
| A 1.3 |
Berechnen
Die Raute A 3B 3C 3D 3 ist ein Quadrat, wenn die Diagonalen [A nC n] und [B nD n] gleich lang sind.
Die Länge der Diagonalen [A nC n] kannst du durch Subtraktion der y-Koordinaten der Punkte C n und A n erhalten, da beide
Punkte den gleichen Abszissenwert x besitzen (vgl. Zeichnung).
yC - yA = -x + 8 - (0,2x - 4)
yC - yA = -1,2x + 12 Somit gilt:
AnCn (x) = (-1,2x + 12)LE
Bedingung für Quadrat:
AnCn =
BnDn
Ferner ist laut Angabentext
BnCn = x LE.
Somit folgt: -1,2x + 12 = x ⇔ -2,2x = -12 ⇔ x = 5,45 ⇒ IL = {5,45}

Sie auf zwei Stellen nach dem Komma gerundet, für welchen Wert von x die Raute A3B3C3D3 ein Quadrat ist.
[Teilergebnis:
AnCn (x) = (-1,2x + 12)LE]
|
3 P |
| A 1.4 |
Unter den Rauten AnBnCnDn hat die Raute A0B0C0D0
den größten Flächeninhalt. Berechnen
Da du bereits die Längen der Diagonalen [A nC n] und [B nD n] in 1.3 berechnet hast,
bestimmst du mit diesen den Flächeninhalt der Rauten wie folgt:
A(x) = 0,5 · AnCn ·
BnDn
A(x) = 0,5 · (-1,2x + 12) · x FE
A(x) = 0,5 · (-1,2x 2 + 12x)FE
A(x) = (-0,6x 2 + 6x)FE
Um A max zu bestimmen, führst du eine Extremwertbestimmung durch:
T(x) = -0,6[x 2 - 10x]
T(x) = -0,6[(x 2 - 10x + 5 2) - 5 2]
T(x) = -0,6[(x 2 - 5) 2 - 25]
T(x) = -0,6(x - 5) 2 + 15
⇒ A max = 15FE für x = 5

Sie diesen größten Flächeninhalt Amax.
|
3 P |
| A 1.5 |
Zeigen Sie durch Rechnung
Da die Diagonalen einer Raute aufeinander senkrecht stehen und
sich gegenseitig halbieren, kann die Länge der Strecke [A nB n]
mit Hilfe des Satzes des Pythagoras im ΔA nB nM nbestimmt werden. Es gilt:
AnMn = (-0,6x +6) LE
und
BnMn = 0,5x LE
AnBn (x) =
(-0,6x +6)2 + 0,5x2 LE
AnBn (x) =
0,36x2 - 7,2x +36 + 0,25x2 LE
AnBn (x) =
0,61x2 - 7,2x +36 LE
Als nächstes setzt du die allgemeine Länge für [A nB n] mit 3 LE gleich:
0,61x2 - 7,2x +36 LE = 3 LE
aus der der Wurzeldefinition folgt:
⇒ 0,61x 2 - 7,2 x + 36 = 9
⇔ 0,61x 2 - 7,2 x + 27 = 0
Für die Diskriminate D erhält man:
D = (-7,2) 2 - 4 · 0,61 · 27 = -14,04
Da D < 0 ist, besitzt die Gleichung keine Lösung.
Daher gibt es keine Raute mit einer Seitenlänge von 3 LE.

, dass sich die Seitenlänge AnBn (x) der
Rauten AnBnCnDn in Abhängigkeit von der Abszisse x der Punkte
An wie folgt darstellen lässt: AnBn (x) = 0,61x2 - 7,2x +36 LE
Weisen Sie sodann rechnerisch nach, dass es unter den Rauten AnBnCnDn keine Raute mit der Seitenlänge 3 LE gibt.
|
5 P |
| A 1.6 |
Einer der Graphen in den untenstehenden Diagrammen a, b und c stellt die Seitenlängen AnBn (x) = y LE
in Abhängigkeit von x dar. Geben Sie das zugehörige Diagramm
an und begründen
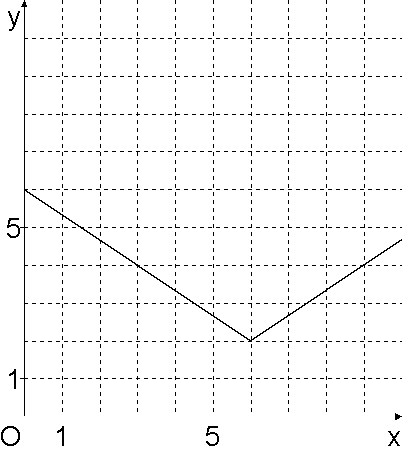
| Diagramm a |
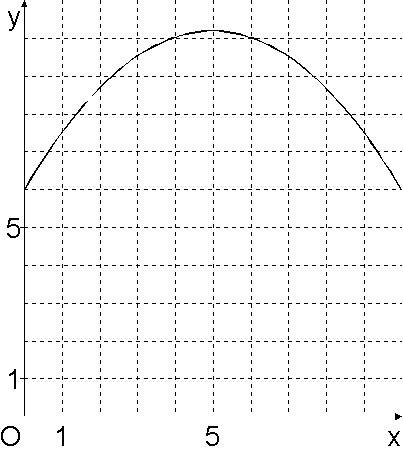
Diagramm b |
Diagramm c |
 |
 |
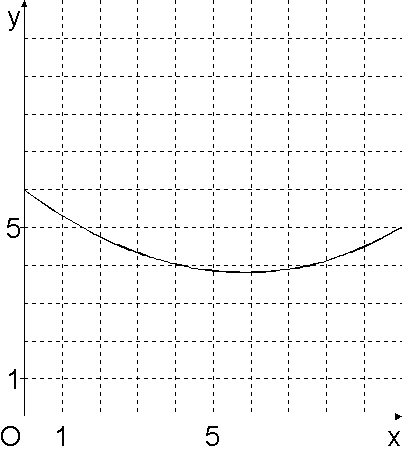 |
Es ist Diagramm c
Diagramm a kann es nicht sein, da es y-Werte gibt, die kleiner als 3 sind.
Nach Aufgabe 1.5 ist dies aber nicht möglich.
Diagramm b kann es nicht sein, da der Graph ein Maximum besitzt, der Term aus Aufgabe 1.5 jedoch nicht.
Sie Ihre Auswahl.
| Diagramm a |
Diagramm b |
Diagramm c |
 |
 |
 |
|
2 P |