-  Geraden zeichnen
 - Geradengleichung
 -   y = |mx| + t
 -   y = |mx + t|
 -   y = ||mx| + t|
 

Die Lösung lässt sich aus einer natürlichen Genese der vorausgegangenen Funktionsgraphen entwickeln.

Vorher haben wir den Graph zur Funktion mit y = | mx | + t entwickelt. 
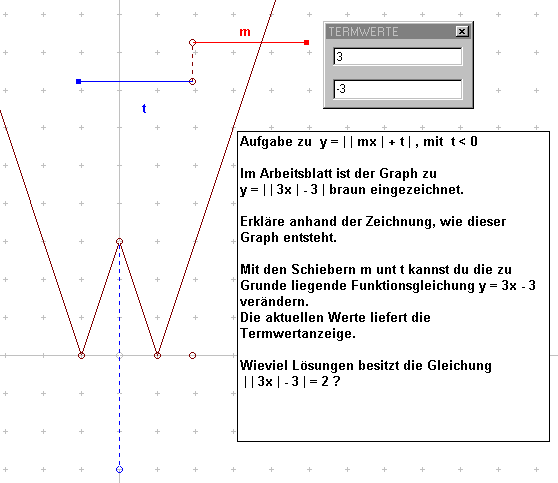
Ausgehend von diesem Graphen ist die Entstehung dieses Graphen zu beschreiben. (vgl. Abbildung)
 
 

Die Beschränkung auf negative Werte für t kann hier angesprochen werden. Ist der Wert für t nämlich positiv, lässt sich die Gleichung y = | | mx | + t | zurückführen auf Aufgaben des Typs y = | mx | + t , der bereits behandelt wurde.

Durch das Einfügen einer Textbox in ein EUKLID - Arbeitsblatt lassen sich gewünschte Aufgabenstellungen in die Zeichnung einbauen.

Näher betrachten wollen wir hier die Teilaufgabe 
'Wieviele Lösungen besitzt die Gleichung y = | | 3x | - 3 | = 2 ?'

In homogener Weise ergibt sich hier ein Zusammenhang zwischen der Diskussion eines Funktionsgraphen mit einer Gleichung.

Die Gleichung  | | 3x | - 3 | = 2  besitzt 4 Lösungen, was eine Parallele zur x-Achse durch (0|2) anschaulich zeigt. Eine algebraische Betrachtung der Gleichung kann sich nun anschließen. Es ergeben sich hier unterschiedliche Ansatzpunkte. 

Aus dem interaktiven Arbeitsblatt lässt ein aus der Konstruktion entwickeltes Kalkül ableiten.

Die x-Koordinaten der Schnittpunkte der jeweiligen Strecken bzw. Halbgeraden mit der Gerade y = 2 führt zu folgendem Ansatz

- 3x - 3 = 2  Ú  3x + 3 = 2  Ú  - 3x + 3 = 2  Ú  3x - 3 = 2 

ó - 3x = 5  Ú  3x = - 1  Ú  - 3x = -1  Ú  3x = 5

ó x = 5/3  Ú  x = - 5/3  Ú  x = 1/3  Ú  x = -1/3

Dieser Lösungsansatz ist losgelöst von einer rein algebraischen Sicht der Lösung einer Gleichung. Er ergibt sich aus der Betrachtung der erzeugten Zeichnung. Damit ist ein Lösungsweg auch dann möglich, wenn rein algebraische Kalküle oder Lösungsschemata nicht eingeübt, nicht präsent oder nicht gewollt sind.

Ein mögliches algebraisches Kalkül könnte wie folgt aussehen:

| | 3x | - 3 | = 2

ó | 3x | - 3 = 2  Ú  | 3x | - 3 = - 2

ó | 3x | = 5 Ú  | 3x | = 1

ó 3x = 5  Ú  3x = - 5  Ú  3x = 1  Ú  3x = -1

ó x = 5/3  Ú  x = - 5/3  Ú  x = 1/3  Ú  x = -1/3

Hier kann sich nun eine Diskussion über die Anzahl von Lösungen einer Gleichung der Art | | mx | + t | = a in Abhängigkeit der Parameter anschließen.