1.3
|
Spiegelung an der x-Achse:
y' = -log3(x' - 1) - 3
Anschließende Parallelverschiebung:
y'' = -log3(x' - 1 + 1) - 3 + 4
f2 mit y = -log3(x) + 1
Einzeichnen des Graphen zu f2.
|
| 1.4
| Einzeichnen der Parallelogramme
Achtung! |
1.5
| Dn = (x + 2) | log3(x + 2 - 1) + 3)
Dn = (x + 2) | log3(x + 1) + 3)
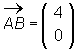
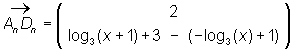
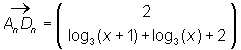
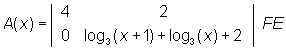
A(x) = 4 · [log3((x + 1) · x) + 2] FE
A(x) = 4 · [log3(x2 + x) + 8] FE
|
1.6
|
4 · log3(x2 + x) + 8 = 20 ,
x > 0,10
<=>
log3(x2 + x) = 3
<=> x2 + x = 33
<=>
x2 + x - 27 = 0 IL = {4,72}
|
|
MI 2003 Aufgabe B1 (Lösung)
| 1.1 |
ID(x) = {x | x > 1} ; IW = IR |
|
1.2 |
| x |
1,1 |
1,5 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
0,90 |
2,37 |
3 |
3,63 |
4 |
4,26 |
4,46 |
4,63 |
4,77 |
|
(c) 2003 Andreas Meier
|