|
A 2.0 |
|
Die Punkte A(1|-1), Bn(3 + 4·cosj
| 1 - 3·sin2j) mit
j Î[0°;123,27°]
und C(5|1) sind Eckpunkte von Vierecken ABnCDn.
Der Punkt S ist der Schnittpunkt der Diagonalen der
Vierecke ABnCDn und zugleich der Mittelpunkt
der Diagonale [AC]. Gleichzeitig teilt der Punkt S
die Diagonalen [BnDn] im Verhältnis
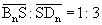 . .
|
|
|
|
|
A 2.1
|
Zeichnen Sie
die Vierecke AB1CD1 für
j = 90°
und AB2CD2 für
j = 60° in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm;
-4 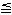 x x 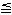 7;
-3 7;
-3 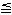 y y 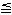 7 7
|
2 P |
|
|
|
A 2.2 |
Die Punkte Bn können auf die
Punkte Dn abgebildet werden.
Berechnen Sie
die Koordinaten der Punkte Dn
in Abhängigkeit von j.
Zeigen Sie
sodann rechnerisch, dass sich die Gleichung
des Trägergraphen p der Punkte Dn in der Form
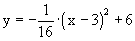 darstellen lässt. darstellen lässt.
[Teilergebnis: 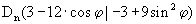 ] ]
Zeichnen Sie
sodann den Trägergraphen p in das Koordinatensystem zu 2.1 ein.
|
5 P |
|
|
|
A 2.3 |
Unter den Vierecken ABnCDn gibt
es ein Drachenviereck AB3CD3.
Zeichnen Sie
dieses Drachenviereck in das Koordinatensystem zu 2.1 ein.
Bestimmen Sie rechnerisch den zugehörigen Wert
für j sowie die Koordinaten
des Punktes B3. (Auf zwei Stellen nach dem Komma runden.)
|
4 P |
|
|
|
A 2.4 |
Zeigen Sie, dass sich der Flächeninhalt
A(j) der Vierecke
ABnCDn in Abhängigkeit von j
wie folgt darstellen lässt:
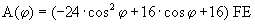 . .
|
4 P |
|
|
|
A 2.5 |
Unter den Vierecken ABnCDn besitzt
das Viereck AB0CD0 den größten
Flächeninhalt Amax.
Berechnen
Sie diesen Flächeninhalt und den
zugehörigen Wert von j.
(Auf zwei Stellen nach dem Komma runden.)
|
2 P |