|
B 3.0 |
|
|
|
|
B 3.1
|
Zeichnen Sie die in 3.0 beschriebene Figur mit ihrer Symmetrieachse
MS und die Parallele P1Q1 im Abstand
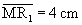 . .
|
1 P |
|
|
|
B 3.2 |
Berechnen Sie, um wie viel Prozent der Kreisbogen
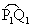 länger ist als die Strecke [P1Q1].
(Auf zwei Stellen nach dem Komma runden.)
länger ist als die Strecke [P1Q1].
(Auf zwei Stellen nach dem Komma runden.)
|
4 P |
|
|
|
B 3.3 |
Unter den gleichschenkligen Dreiecken PnQnM gibt es
ein gleichseitiges Dreieck P2Q2M.
Zeichnen Sie das Dreieck P2Q2M in die
Zeichnung zu 3.1 ein.
Berechnen Sie den Flächeninhalt
der von der Strecke [P2Q2] und dem
Kreisbogen 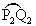 begrenzten Fläche.
(Auf zwei Stellen nach dem Komma runden.) begrenzten Fläche.
(Auf zwei Stellen nach dem Komma runden.)
|
3 P |
|
|
|
B 3.4 |
Die von der Strecke [AB] und dem Kreisbogen
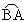 begrenzte Figur und die Dreiecke PnQnM rotieren
um die Symmetrieachse MS.
begrenzte Figur und die Dreiecke PnQnM rotieren
um die Symmetrieachse MS.
Berechnen Sie den Oberflächeninhalt der Halbkugel.
Die durch die Rotation entstehenden Kegel haben den
Grundkreisradius 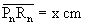 mit 0 < x 7; xÎIR.
mit 0 < x 7; xÎIR.
Zeigen Sie, dass sich der
Oberflächeninhalt A(x) der Kegel in Abhängigkeit von x
wie folgt darstellen lässt:
A(x) = p · (x2 + 7x)cm2
|
3 P |
|
|
|
B 3.5 |
Berechnen Sie
die Belegung für x auf zwei Stellen nach dem Komma
gerundet, für die der Oberflächeninhalt A(x) des
zugehörigen Kegels halb so groß ist wie der
Oberflächeninhalt der Halbkugel.
|
3 P |
|
|
|
B 3.6 |
Berechnen Sie
jeweils auf zwei Stellen nach dem Komma gerundet den
Grundkreisradius 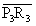 und den Oberflächeninhalt A3 für denjenigen Kegel,
bei dem im Axialschnitt P3Q3M das Maß des Winkels
P3MQ3 130° beträgt.
und den Oberflächeninhalt A3 für denjenigen Kegel,
bei dem im Axialschnitt P3Q3M das Maß des Winkels
P3MQ3 130° beträgt.
|
2 P |
|