Wie zeichne ich eine Parabel ausgehend von der
allgemeinen Gleichung y = ax² + bx + c?

Das Zeichnen einer beliebigen Parabel mit der Gleichung y = ax² + bx + c wird mit Hilfe eines MAKROS realisiert.

Sie können parabel.mak hier downloaden.
Dieses MAKRO 'Parabel' liegt jedem Schüler vor, in der Handhabung dieses Makros wird der Schüler durch ein Informationsblatt eingeführt.

An einem Beispiel möchte ich die Schülervorgehensweise erläutern.

Zeichnen Sie eine Parabel mit der Gleichung y = . G = IRxIR.

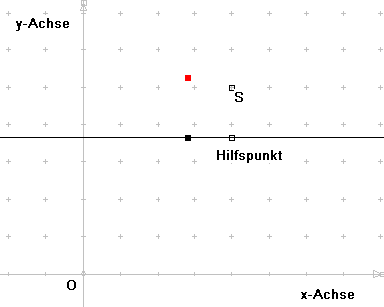
  • Der Schüler ermittelt zuerst analog zum herkömmlichen Unterricht den Scheitelpunkt S(4|5) der Parabel. Diesen zeichnet er in das EUKLID-Blatt ein.

    Er berechnet nun ausgehend von den Scheitelpunktskoordinaten und dem Faktor a die Koordinaten des Hilfspunkts H (vgl. mathematischer Hintergrund).

    Formel: , wobei . Für unser Beispiel:

    Dieser errechnete Wert wird nun von der y-Koordinate des Scheitels S(4|5) subtrahiert.
    Dies bedeutet nun also, dass sich die Koordinaten von H als ergeben.

  • Er zeichnet nun eine Parallele durch den Hilfspunkt zur x-Achse und legt einen Punkt auf diese Gerade.

    • <Makro> - <Parabel> anschließendes Anklicken des Scheitelpunktes S, des Hilfspunkts und des variablen Punkts auf der Parallelen zur x-Achse durch den Hilfspunkt.

  • Das MAKRO 'Parabel' erzeugt dann einen Punkt der zu zeichnenden Parabel.
  • Anschließend kann die Parallele und der Hilfspunkt verborgen werden
    (Doppelklick mit der rechten Maustaste auf das jeweilige Objekt).
  • <Verschiedenes> - <Ortslinie aufzeichnen> führt dann zur gewünschten Parabel.


Beispiele zur Berechnung von H(4|y) für verschiedene Parabeln mit S(4|5)

p mit y = a (x - 4)² + 5

a = 1 => H(4|4,75)
a = 2 => H(4|4,875)
a = -0,5 => H(4|5,5) usw.


(c) Andreas Meier